Stochastic Modeling of COVID-19: A SEIAISQR-type model

C. U. Chikwelu; F. Ewere; J. I. Mbegbu

PDF

Published: 2025-11-25

Keywords:

Milstein’s Higher Order Method, Lyapunov Function, SEIAISQR Model, COVID-19, Stochastic Model

C. U. Chikwelu

Department of Statistics, Faculty of Physical Sciences, Nnamdi Azikiwe University, Awka, Nigeria

F. Ewere

Department of Statistics, Faculty of Physical Sciences, University of Benin, Benin City, Nigeria

J. I. Mbegbu

Department of Statistics, Faculty of Physical Sciences, University of Benin, Benin City, Nigeria

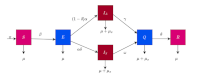
Abstract

This paper presents a model for the Corona-Virus (COVID-19) disease taking into account random perturbations. The proposed model is composed of six different classes namely the Susceptible population, the Exposed population, the Asymptomatic infectious population, the Symptomatic Infectious population, the Quarantined population and the Recovered population (SEI_AIS_QR). Using appropriately formulated stochastic Lyapunov functions, we established sufficient conditions for the existence and uniqueness of the positive solutions to the model. The condition for the extinction of the disease is also established. Numerical simulations are applied to illustrate the analytical results obtained herein.The reproduction number was obtained as R₀ ^S = 0.2585 < 1 and R₀ ^S = 2.4423 > 1 which show that the stability analysis of the equilibrium point is locally asymptotically stable whenever the basic reproduction number R₀ ^S < 1 and unstable
whenever R₀ ^S > 1.

Downloads

Download data is not yet available.

Issue

Vol. 7 No. 1 (2024)

Section

Articles

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

How to Cite

Chikwelu, C. U., Ewere, F., & Mbegbu, J. I. (2025). Stochastic Modeling of COVID-19: A SEIAISQR-type model. Benin Journal of Statistics, 7(1), 29– 43. https://www.bjs-uniben.org/index.php/home/article/view/45

References

Din, A., Khan, A., and Baleanu, D. (2020). Stationary distribution and extinction of stochastic coronavirus (covid-19) epidemic model. Chaos, Solitons Fractals, 139, 110036.

Ding, Y., Fu, Y., and Kang, Y. (2021). Stochastic analysis of covid-19 by a seir model with levy noise. Chaos: An Interdisciplinary Journal of Nonlinear Science, 31(4), 043132.

Higham, D. J. (2001). An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM review, 43(3), 525–546.

Lai, C.-C., Shih, T.-P., Ko, W.-C., Tang, H.-J., and Hsueh, P.-R. (2020). Severe acute respiratory syndrome coronavirus 2 (sars-cov-2) and coronavirus disease-2019 (covid-19): The epidemic and the challenges. International journal of antimicrobial agents, 55(3), 105924.

Mao, X. (1997). Stochastic differential equations and their applications, horwood, chichester, 1997. MR1475218.

Perko, L. (2013). Differential equations and dynamical systems (Volume 7). Springer Science & Business Media.

Wu, Z., and McGoogan, J. M. (2020). Characteristics of and important lessons from the coronavirus disease 2019 (covid-19) outbreak in china: Summary of a report of 72314 cases from the chinese center for disease control and prevention. jama, 323(13), 1239–1242.

Article Sidebar

Main Article Content